有限元分析进行产品设计计算,多半是根据现有机型编制针对实际的有限元强度分析计算程序进行的。已有的有限元计算通用程序如SAPS程序都是研究整体对象。实际研究的绝大多数问题是形体不规则且较复杂,所划分的单元及节点数较多,出现了小型计算机内存溢出。采用子结构法对箱形结构进行偶合分析计算,实现单元及节点数较多的结构有限元分析,以解决大型复杂结构与小型计算机内存不足的问题。
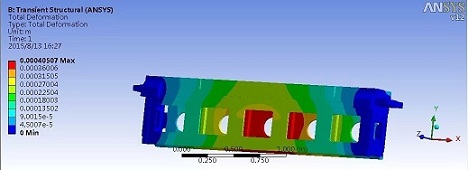
由于箱形结构上有许多轴孔而形成计算较为复杂的结构。采用三维20节点等参数单元来划分箱形结构的离散网络,以适应曲线或直线边界以及曲面或平面边界,较好地逼近实际结构的形体。但形成了高阶的整体刚度矩阵,极有可能超出计算机容量,在小型计算机上难于实现计算。为此,将箱形结构划分为三个子结构,如图所示。每个子结构单独建立力学模型,再进行有限元稠合分析计算。
依据线弹性结构的叠加原理把各子结构边界固定,在子结构内部节点载荷作用下求出边界节点反力;再把边界放松,置内部节点载荷为(O),由边界上力的平衡方程求出真实边界位移;然后分别对每一子结构进行分析。即将整体结构划分为子结构,各子结构之间通过边界位移来藕合,计算出边界节点位移后,各子结构便相互独立。式中节点位移向量及载荷向量。
为确定子结构法计算程序FES的计算误差,对箱形结构进行了应变测量。按子结构法划分的节点处布置45。应变其中选择内部节点和边界节点各10个测点。试验载荷按静态加载由测力传感器测控加载大小。应变实验装置采用YJ-5型静态变变仪和P20R-5型预调平衡箱构成多点测量系统。测量线路采用半桥连接,其中一个为温度补偿片。主要测点应变换算成应力的测试结果与子结构法有限元计算程序FES计算结果及其误差见表结果表明,最大计算误差为18.19%。
(1)测试结果表明,子结构法计算程序FES计算结果与实测值基本一致,说明子结构计算模型与程序FES正确,其计算误差满足工程计算要求。
(2)所研究的箱形结构安全贮备量较大。
(3)子结构法为在小型计算机上计算大型复杂结构,尤其是组合结构件的强度问题,提供了应用前景。
(4)分块网络划分简单、数据准备工作量较小,节省内存单元且可减少计算时间。
专业从事机械产品设计│有限元分析│强度分析│结构优化│技术服务与解决方案
杭州那泰科技有限公司
本文出自杭州那泰科技有限公司www.nataid.com,转载请注明出处和相关链接!

 手机直线:
手机直线: 咨询热线:0571-56211150
咨询热线:0571-56211150







