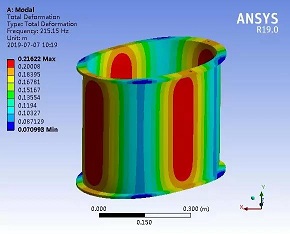
放入式电子测压器用于测试火炮发射时膛压曲线，由于工作在高温高压环境，必须用高强度壳体对测压器电路模块进行可靠保护。测压器受许多因素的影响，希望体积可能的小，测压器保护罩的尺寸和体积也应尽可能的小，受测压器的影响，保护罩的形态袋是一个厚壁圆筒。为了减小测压器保护罩体积，就要尽可能减小壁厚，因此，就要选择合适强度理论对其进行强度有限元分析，求出弹塑性极限荷载。
      目前，对于大量的工程结构，采用Tresca Mices等准则进行弹塑性极限分析，将产生较大的误差。由于没有考虑中间主应力的影响，与试验结果有差距，它只适用于剪切强度极限几与拉伸强度极限和压缩强度极限的关系。双剪强度理论虽然考虑影响，但它也只能适用于材料。Mices准则虽然考虑了中间主应力，并且也得到广泛应用，但20世纪60年代以来的大量实验发现，Mices准则应用到岩石力学、土力学会产生很大的误差，Mises屈服准则也只能适用于拉压强度相同的某些金属类材料。
      近年来，国内外学者开始考虑拉压强度不相等对极限荷载的影响，采用不同准则进行某些问题的极限荷载分析，得出了一些较好的结论。为了寻求适用于更广泛的各种材料的极限荷载分析，本文采用俞茂宏统一强度理论对受外压的厚壁圆筒进行弹塑性极限分析，求得了统一极限解。它考虑拉压强度不相同以及影响，可以更好地适用于各种材料的结构极限荷载分析，对于解决该类结构的合理设计和减轻重量都有重要意义。
      本文采用俞茂宏统一强度理论对测压器保护罩(厚壁圆筒受外压作用)进行了塑性极限荷载分析，得出了统一解的计算公式。在该式中，可得出极限解。取结果为双剪强度理论的极限解，当QT趋近1时，结果为Tresca解。对于不同的材料，取定T用式计算出b值代入式，即可求出相应的极限荷载。采用俞茂宏统一强度理论，可以充分发挥材料的强度潜力，减小厚壁筒的壁厚，大大节约材料，并减轻结构重量。

                                                                                专业从事机械产品设计│有限元分析│强度分析│结构优化│技术服务与解决方案
                                                                                                                                                      杭州那泰科技有限公司
                                                                              本文出自杭州那泰科技有限公司www.nataid.com，转载请注明出处和相关链接！