碟形弹簧是用金属板或锻压坯料制成的截锥形压缩弹簧，具有轴向尺寸小、刚度大、变刚性等特点。普通碟形弹簧（以下简称普通碟簧）可以分为无支撑面和有支撑面两种，主要用于缓冲和减震的场合。普通碟簧的载荷-变形关系数值解常用的理论计算方法是Almen-Laszlo（简称A-L）解析法，该法忽略了挠曲变形的影响，只适用于R/r较大、h/t较小的场合。现行国标的载荷-变形计算也正是采用此计算方法。而对于法兰接头用碟形弹簧（以下简称本文碟簧）的设计计算，A-L法并不适用。
      本文碟簧适用于法兰接头连接的场合，尤其是当法兰接头连接件长期处于高温环境下工作或受到温度和压力波动时，必然会导致螺栓和垫片等重要部件产生塑性变形，从而降低了螺栓的预紧载荷，也降低了垫片应力。当垫片应力降低到一定程度而不足以维持其密封状态时，则发生泄漏。为了解决上述问题，考虑在螺母与法兰之间适当地加装本文碟簧，如图所示。当系统发生塑性变形时，本文碟簧将释放变形能，以有效地补偿螺栓的预紧载荷，阻止垫片应力的降低，继续维持法兰接头的良好密封性能。
      普通碟形弹簧的力学模型与参数符号如图所示，令D=2R，d=2r。由于本文碟簧与普通碟簧的用途不同，决定了其结构尺寸、载荷-变形特性的不同。例如，本文碟簧的径向尺寸更小、碟片厚度更大，h/t=0.05～0.1，D/t<12，D/d≈1.75；而国标中的普通碟簧尺寸参数范围为h/t=0.4、0.75、1.3，D/t=18、28、40，D/d≈2.0，附录B（非常用碟簧尺寸系列）也并未包含适合法兰接头用碟簧的尺寸系列。
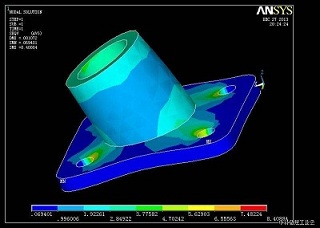
      碟簧的有限元分析模型如图所示。图是本文不计摩擦时的二维轴对称有限元模型，在右下端的支点处固定其轴向位移，径向约束自由，在左上端点施加轴向载荷，采用多载荷步求解。此模型在以前的诸多文献中大有所在。有限元采用二维轴对称平面单元Plane82。图是本文计及摩擦时的二维轴对称有限元模型，中间处是碟簧模型，上、下处是刚性平台模型，有限元采用二维轴对称平面单元Plane82，与碟簧接触处加入点面接触单元Conta175，摩擦系数0.3。下刚性平台的下端固定，上刚性平台施加适当的约束，只允许相对于下刚性平台平动（靠近或远离）；在上刚性平台的上端施加载荷，也采用多载荷步求解。加上、下刚性平台模型有如下好处：（1）可以模拟存在摩擦力的情况；（2）碟簧的受力特点较接近试验平台以及实际应用装置。这样的有限元模型主要是针对本文碟簧摩擦力不可忽略的情况。
      ANSYS有限元软件对碟簧模拟的验证模拟值如表1中FEA之列所示，A-L公式计算值如表1中A-L公式之列所示，分别将其与精确解做比较，并分别计算相对误差。求解过程都只考虑弹性变形。
      有限元模型及边界条件如图所示，Di为碟簧内径，Do为碟簧外径，t为碟簧厚度，h为自由高度。E＝2.06×105MPa，μ＝0.3。上述的几款碟簧很具有代表性，其载荷-位移曲线包括了单调递增的非线性曲线、接近线性的曲线以及具有负刚度的曲线。从大量的有限元模拟数据来看，ANSYS对碟簧的非线性曲线的模拟十分准确，可以用作设计参考。

                                                                                专业从事机械产品设计│有限元分析│CAE分析│结构优化│技术服务与解决方案
                                                                                                                                                      杭州那泰科技有限公司
                                                                              本文出自杭州那泰科技有限公司www.nataid.com，转载请注明出处和相关链接！