随着技术的迅速发展，可穿戴设备将会对我们的生活带来很大转变。而可延展可弯曲的柔性电子器件，由于能满足人们对电子产品的可变性、便携等要求，将会在电子产业发挥不可替代的支柱性作用。其中最重要的是使薄膜器件的电学性能在大变形中维持在相对稳定的水平。为了提升功能薄膜的可变形性，科学界从力学性质入手提出了几个策略。
      例如，硅和砷化镓的半导体带能以正弦曲线周期的皱褶或扣环的方式集成在弹性基底上，这种皱褶或扣环是一种可拉伸结构，能够适应大的拉伸或压缩位移。另一个可伸缩的结构是由功能薄膜器件组成孤立的刚性群岛，配以薄的金属薄膜的蛇形线连接。功能薄膜的蛇形结构的设计能大大增加薄膜的可延展性。鲁南姝在聚酰亚胺上溅射ITO的蛇形线，研究了不同尺寸蛇形线结构的力学和电学性质变。Rogers团队成功将2维功能薄膜转变成了3维的结构，相比于原有的2维结构，这种新的3维结构能够适应更大程度的拉伸和弯曲，从而使制得的柔性器件具备更强的稳定性。
      然而，对于柔性基底本身的研究还较少。笔者首次从基底的角度，通过有限元分析，提出了改善基底的大应变性能的方案。大应变、轻便性好的基底材料对于柔性基底将会起到重要的作用，具有广泛而实用的价值。其中聚二甲基硅氧烷(PDMS)具有极好的生物亲和性、化学惰性和低弹性模量，可以在不破坏结构的情况下承受极大的机械形变，是理想的大应变柔性基底材料。通过改变PDMS的配比，调整基底的弹性模量和泊松比，从而对其拉伸性进行调控。
      本文采用有限元及位移法，利用Abaqus，对矩形PDMS薄板在水平均匀位移载荷下的应变模态进行仿真，绘制不同配比时的应力-应变的变化关系，进而计算出柔性基底的受力和形变关系，得到具有更好大应变性能基底的方法。
      超弹性(hyperplastic)是指材料存在一个弹性势能函数，该函数是应变张量的标量函数，其对应变分量的导数是对应的应力分量，表示在卸载时应变可自动恢复的现象。应力和应变不再是线性对应的关系，而是以弹性能函数的形式一一对应。
      PDMS拉伸极限较大，应力很难超过它的拉伸极限。PDMS在外力撤去后一般仍能恢复原有的形状和尺寸，故不认为它超过弹性极限，可认为它的应力-应变曲线取线性变化阶段。在计算过程中，把PDMS的材料性质定义为超弹性。
      鉴于超弹性是描述一种应力应变关系非线性的材料的一种模型，常见的超弹性模型有StVenant-Kirchhoff模型、Fung模型、Mooney-Rivlin模型、Ogden模型等，本模拟中应用的是Mooney-Rivlin模型。
      根据有限元分析的思想，模拟中将矩形基板划分为有限个特定体积的小单元，并对每个小单元进行数值分析。故在以下的应变分布以及应力-应变关系的分析中，以等间距法选取一些具有代表性的小单元。具体表现为：先选取一列目标单元并记录其标签，再按照等间距的方法选取具有代表性的小单元的标签，输出这些标签并带入分析。这样做既能保证结果具有代表性，又能大大简便运算量，提高结果分析的效率。
      采用Abaqus软件对柔性基板进行有限元分析，具体步骤如下：
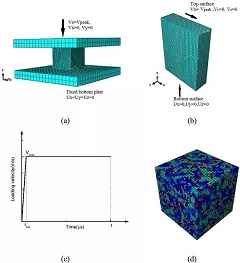
      (a)建立模型。参数设置为：长度100mm，宽度40mm，厚度5mm，E=1.8MPa，v=0.48。将材料的性质参数转化为Mooney-Rivlin模型中的C10、C01和d，则C10=0.243243，C01=0.060811，d=0.133333。(b)定义载荷。结构两侧均施加拉位移10mm，其余方向为初始状态。(c)划分网格。将模型按照近似尺寸为0.5mm进行划分，得到个数为200×40×5的网格，便于下一步的有限元分析。(d)设置分析步，建立作业，提交分析。(e)输出结果，记录并分析。从表述PDMS基板应变模态分布的图可以看出，在基板不同位置，其应变模态是不同的。下面将讨论不同位置的应变分布。
 

                                                                                专业从事机械产品设计│有限元分析│CAE分析│结构优化│技术服务与解决方案
                                                                                                                                                      杭州那泰科技有限公司
                                                                              本文出自杭州那泰科技有限公司www.nataid.com，转载请注明出处和相关链接！