三维编织复合材料通过增强长纤维束在空间相互交织成一整体，克服了层合复合材料层间强度低、易分层的缺陷，具有抗冲击、损伤，疲劳能力强，结构可设计性好的优点，因而引起了力学和材料科学研究者的高度重视。影响编织复合材料力学性能的最重要的因素是它的编织角，编织角越小，材料的应办应变曲线越接近于线性；大编织角复合材料的应办应变曲线表现出明显的非线性性质。本文主要针对大编织角复合材料的细观破坏机理进行了较深入的研究，并建立了较为合适的细观强度失效判据。
      早期的三维编织复合材料力学性能的理论研究大多以刚度分析为主，研究其平均的力学性能。事实上，由于材料本身具有高度的细观非均匀性，使得材料的应力在细观很小的尺度内却发生很大的变化，宏观力学性能无法反映细观应力波动，不利于进行强度有限元分析。近年来，Tao Zeng采用混合单元法对材料的细观力学性能进行研究，这种方法考虑了细观力学参数的不均匀性，对于材料的失效分析具有一定的参考价值，然而在建模过程中忽略了表面和角柱区域效应的影响，对于细观分析精度有一定的影响。冯林采用均匀化方法预报了材料的等效弹性性能，这种方法通过定义宏观和细观两个尺度的参量将任一细观参数场表示为宏观和细观两种参数的表达式，然后通过宏细观有限元相结合的方法可以较为方便地模拟出细观参数场的分布。本文采用均匀化方法对材料三种单胞结构的细观应力分布进行了数值模拟，所得的强度分析结果与实验分析结论较为相符。
      均匀化方法是一种基于小参数渐近展开的多尺度摄动方法，用以表达某种宏观参数的细观响应的数学方法。由于三维编织复合材料是由几种周期性分布的细观单胞组成，其应力分布在细观尺度很不均匀，因此运用此方法可以较好地解决细观应力场的分布问题。
      下而就均匀化方法及其有限元求解过程作简要介绍。
      首先，引入小参数￡及宏观和细观两种尺度坐标X和y，其中将非均匀位移场、应变场和应力场表示为￡的渐近展开式。
      于是可以通过细观有限元的方法求出等效位移，并可代入式求出材料的等效弹性模量，使其化为均质材料，然后用宏观有限元的方法求出宏观位移。代入式便可以求出材料内部任一点的应力值了。
      根据纤维束在织物内部、表面和角柱处路径的不同，可将材料分为内胞、而胞和角胞三种单胞模型。对三种单胞分别划分单元，得到的单胞的有限元模型如图所示(为清晰起见，只显示纤维束单元)。
      本文采用文献的实验数据，基体(TDB 85环氧树脂)为各向同性材料，纤维(T300碳纤维)为横观各向同性材料，单丝直径纤维束为N=6000，内部编织角x=410，纤维体积百分含量为V=0.54，其中纤维和基体的弹性常数如表所示。在计算过程中采用如下几点假设：(1)由于纤维束在形成过程中有大量孔隙的存在，以致注胶过程中在纤维束中也渗进部分基体，分析起来较为复杂本文假定纤维束为圆形实心体，其等效直径D可由下式确定。
      基体TDB 85环氧树脂为非线性粘弹性材料，其非线胜过程较为复杂，尚无统一的应力应变关系曲线，这里采用文献的实验本构关系，如图所示。
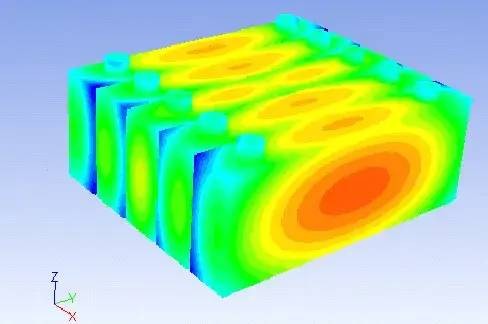
      采用以上两点假设，用均匀化方法加上周期性的边男条件进行有限元求解，可模拟出三种单胞的应力分布图三为在拉伸极限强度下，三种单胞中纤维的正应力分布图，图为剪应力T分布图。

                                                                                专业从事机械产品设计│有限元分析│CAE分析│结构优化│技术服务与解决方案
                                                                                                                                                      杭州那泰科技有限公司
                                                                              本文出自杭州那泰科技有限公司www.nataid.com，转载请注明出处和相关链接！