工程结构有限元分析误差包含模型误差和计算误差。模型误差是将实际问题抽象为适合计算机求解的有限元模型时所产生的误差，即有限元模型与实际问题之间的差异，它包括有限元法离散处里所固有的原理性误差，也可能包括几何模型处里，实际工况量化为模型边界条件时所带来的偶然性误差，计算误差是指采用数值方法时利用有限元模型进行计算所产生的误差，误差性质是舍入误差和截断误差，基于此，提出的工程校验方法及有限元误差数学表达式，对提高有限元分析精度和准确性提供帮助。
      模型质量的工程校验网格数量增加，有限元分析精度一般会随之增加，但当网格数量太大时，有限元计算的累积误差反而会降低计算精度。另外，当网格数量增加时，单元形成、网格划分和方程求解时间也会增加，所以合理选择单元，控制网格密度也是校验模型质量的主要方法之一，参考文献叙述的校验模型方法，有的在理论上虽然可行，但实施起来却很困难，然而即使做了上述的模型校验步骤，也不能作为定量判断有限元模型质量好坏的方法，工程上，最直接的是从计算结果值来判断模型及单元选择的好坏，以下给出一种工程快捷判断模型质量方法：
      a、对工程问题以某一合适的尺度初次进行网格划分，进行分析计算。
      b、将单元的尺寸减少一半，或者把低阶单元换成高阶单元网格划分后，再计算。
      c、比较单元改变前后同一地方的应力值。
      d、如果应力值相差50%，原来的单元选择和划分就有50%的不合适，因此，要考虑重新网格划分或单元选择。
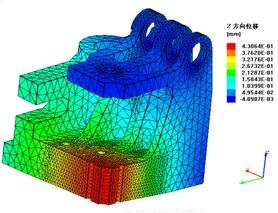
      e、重复步骤a～d，直到2次应力值之差小于50%，可以认定网格划分尺度或选择单元合适，此时的有限元分析在工程上可以接受，例如，一个平面一边固支，一边受力，在材料参数、边界条件都不改变的情况下，改变单元尺度，即每边分别2，8，16等份，3种网格密度计算所得的最小von Mises stress处于平面右上角处，如图所示的数值处。
      从图中可以看出，对应点的应力相差大于50%，根据以上方法，每边等分2份的网格划分不合理，但是，应力变化幅度较小，相同点的最小应力互差为5-8%，故每边等分8份的网格划分认为是合理。
      以上例子表明，这种工程校验方法对于计算规模不是很大的有限元分析是一种有效方法，但对于分析精度高和规模大的问题，可能就显得力不从心，因此，可以应用误差估计方法来校验。

                                                                                  专业从事机械产品设计│有限元分析│强度分析│结构优化│技术服务与解决方案
                                                                                                                                                  杭州纳泰科技咨询有限公司
                                                                          本文出自杭州纳泰科技咨询有限公司www.nataid.com，转载请注明出处和相关链接！